A couple of weeks ago I covered factoring in my College Algebra class, which we’ll mainly use for working with quadratic equations. This always makes me think about a method for factoring quadratics that I’d never seen before moving back to New York state. Years ago, I looked it up on what I think was an NYS Department of Education website which called it the “AC method” for factoring quadratics. When I tried to find this again, I only found it on YouTube called “slide and divide” and the “Berry Method.” Both of those names seem unnecessarily arcane to me, but for this post, I’ll call this process “slide and divide.” The references to an “AC Method” that I say today were actually talking about the “grouping number method” which we’ll come back to.
I hope that the fact that it’s become difficult to find references to what I think of as the AC Method is evidence that it’s going away. It needs to.
When I was in high school, I remember that factoring quadratics that looked like  was pretty straight forward when
was pretty straight forward when 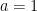 , but when
, but when  was different from
was different from 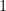 it got trickier. The only tool we were taught was trial and error, but you need to develop some intuition to use trial and error efficiently. Both the grouping number method and slide and divide attempt to give students a systematic process that builds on the experience of the
it got trickier. The only tool we were taught was trial and error, but you need to develop some intuition to use trial and error efficiently. Both the grouping number method and slide and divide attempt to give students a systematic process that builds on the experience of the 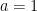 case to help them with the
case to help them with the 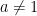 case. If you’re a mathematician, and you’ve seen the slide and divide approach, you probably found it horrifying. I know I did. It goes something like this: say you want to factor the following polynomial.
case. If you’re a mathematician, and you’ve seen the slide and divide approach, you probably found it horrifying. I know I did. It goes something like this: say you want to factor the following polynomial.
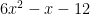
You begin by replacing the leading coefficient with 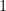 while replacing the constant term with the product of itself and the leading coefficient.
while replacing the constant term with the product of itself and the leading coefficient.
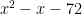
Why do we do this? I’m not sure it’s ever made clear. But this is a lot easier to factor since the leading coefficient is one. We just need to find two factors of 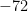 that add up to the coefficient of the middle term,
that add up to the coefficient of the middle term, 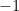 , namely
, namely 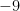 and
and  . These become the constant terms of the factors
. These become the constant terms of the factors
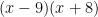
We then replace each  with
with  …
…
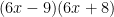
…and then remove the common factor from each binomial.
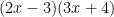
With that, our quadratic polynomial is factored.
The single redeeming feature of this process is that it actually works, but think about these steps. Where did the 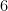 in front of the
in front of the 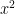 go? Why does it make sense to multiply it into the
go? Why does it make sense to multiply it into the  ? For that matter, why do the
? For that matter, why do the  s magically reappear? And why is it okay to just cancel the common factors from the penultimate step? If I thought about it for a moment, I bet I’d actually have even more questions.
s magically reappear? And why is it okay to just cancel the common factors from the penultimate step? If I thought about it for a moment, I bet I’d actually have even more questions.
I’ve had a few students who wanted to use this method to factor, but none of them was ever able to explain why it works. That’s the ultimate problem with this method. It’s a list of meaningless steps that, once forgotten, will be gone forever because it doesn’t attach to any understanding. If you teach mathematics, it’s incumbent upon you to make your material meaningful to your students. Some people naively believe that this means you have to teach mathematics in a context that is directly relevant to the students’ interest, but in my opinion, that’s not true. You need to help them understand what’s happening and why it’s being done. Each step should have a clear and understandable rationale that helps to drive the process forward. Slide and divide does none of these things.
This process is not irredeemable, however. It is possible to work slide and divide in a way that gives it these characteristics. Let’s go through this in our original example.
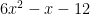
The idea behind this method is that, if we can rewrite the polynomial with a leading coefficient of one, it will be easier to factor. To do this we need the leading term to be a perfect square. We can make that happen by multiplying the polynomial by 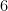 . Because we don’t want to change the polynomial, we’ll divide by
. Because we don’t want to change the polynomial, we’ll divide by 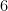 at the same time.
at the same time.

A simple substitution will give us a leading coefficient of 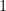 . We define
. We define 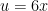 .
.

Just like we did above, to factor our numerator we need two factors of 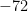 that add up to
that add up to 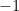 , that’s still
, that’s still 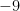 and
and  .
.

To get back to expressions that involve  s, we undo the substitution. That makes it clear why the
s, we undo the substitution. That makes it clear why the  s return.
s return.

And now, we’d like to get rid of the 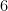 s since we don’t need them any longer. Where did the
s since we don’t need them any longer. Where did the 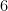 in the numerator go? It’s inside the common factors of the two binomials. We can factor those out…
in the numerator go? It’s inside the common factors of the two binomials. We can factor those out…
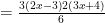
…and they clearly cancel with the 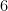 in the denominator. That leaves us with our answer.
in the denominator. That leaves us with our answer.
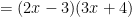
That’s pretty cumbersome and so slide and divide leads you to a no-win-scenario. The quick way doesn’t engender understanding while the more rigorous approach isn’t quick.
So, what should we teach instead? The grouping number method that I mentioned earlier. To set it up, let’s think about what happens in the following polynomial multiplication.
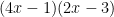
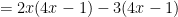
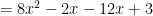
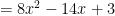
Normally, you’d just skip the second step, but it’s important to realize that what you’re really doing is using the distributive property twice. Additionally, let’s think about the -12 and the -2. It’s clear that they add up to the final coefficient of x, but it’s also true that their product (-12)(-2) = 24 is the same as the product of the leading coefficient and the constant term, (8)(3). Notice this has to be true. In either case, it’s the product of 4, -1, 2 and -3, merely in a different order.
So, how do we go in the other direction? That is, how do we factor instead of multiply? We’ll demonstrate the grouping number method on the polynomial  .
.
The grouping number of a quadratic polynomial is the leading coefficient multiplied by the constant term.
So, in this case, it would be 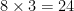 .
.
Next, you want to look for two factors of your grouping number that add up to the coefficient of  . In this case,
. In this case,  and
and  . We use these two numbers to rewrite the middle term to get the following.
. We use these two numbers to rewrite the middle term to get the following.
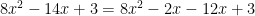 .
.
In other words, to rewrite the polynomial in this way, you find two factors of your grouping number that add up to the coefficient of  and use those to break down the middle term.
and use those to break down the middle term.
Why rewrite the polynomial in this way? Because it sets us up perfectly to factor by grouping.
Factoring by grouping is a technique for factoring a polynomial with four terms. In a nutshell, to factor by grouping, you remove the greatest common factor from the first two terms, then remove the greatest common factor from the last two terms. If the resulting binomial factors are the same you can factor this out to get the product of two binomials. Notice, that’s using the distributive property twice, just in the opposite direction as before.
Therefore, to finish factoring the polynomial we can factor by grouping.


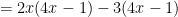
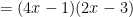
Notice this exactly reverses the steps of the multiplication with which we started.
In short, as long as you have no common factors, the quadratic polynomials where the grouping number can be factored into two numbers that add up to the middle coefficient are exactly the ones that can be factored by grouping. All the others are prime.







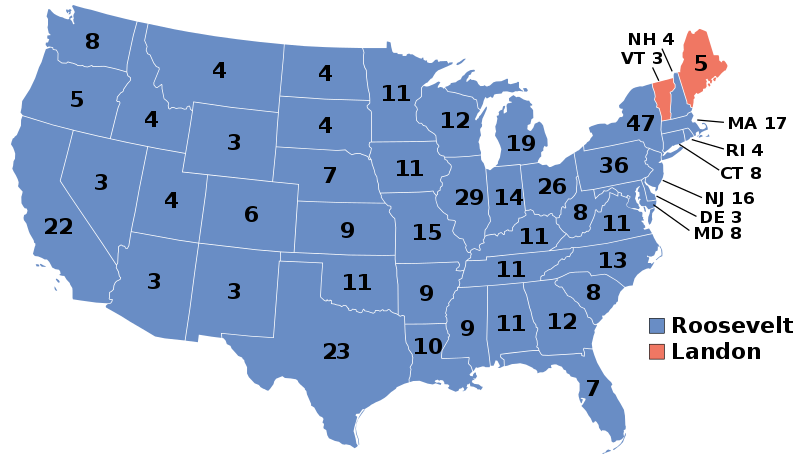


 I have some intense opinions about politics and generally, I’m happy to engage. But I don’t want to make this a blog about politics. If someone stumbles on this blog wanting to read about comics or mathematics or whatever they may not be interested in my opinions about candidate X or birthright citizenship or the current occupant of the Oval Office. And that should be fine. Some politics may sneak in from time to time but I’d like this to be a place that’s free from the most divisive arguments we’ve seen in my lifetime.
I have some intense opinions about politics and generally, I’m happy to engage. But I don’t want to make this a blog about politics. If someone stumbles on this blog wanting to read about comics or mathematics or whatever they may not be interested in my opinions about candidate X or birthright citizenship or the current occupant of the Oval Office. And that should be fine. Some politics may sneak in from time to time but I’d like this to be a place that’s free from the most divisive arguments we’ve seen in my lifetime.
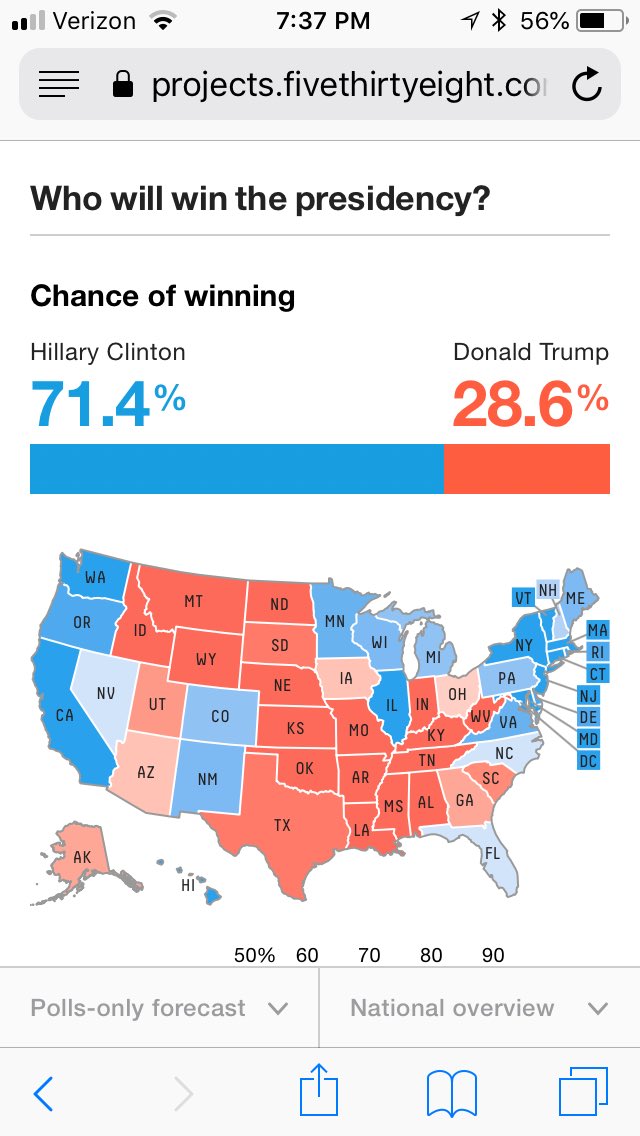 I see this graphic on Twitter a lot in Nate Silver’s feed. The implication being made that Silver “predicted” that Clinton would win the White House and so, 538 “got it wrong.” That’s not what this says at all. This is a probability. What this says is that, if you could repeat the election a bunch of times, Clinton would only win about 71.4% of the time. In 28.6% of the “elections” Trump would be elected. A Trump election isn’t surprising.
I see this graphic on Twitter a lot in Nate Silver’s feed. The implication being made that Silver “predicted” that Clinton would win the White House and so, 538 “got it wrong.” That’s not what this says at all. This is a probability. What this says is that, if you could repeat the election a bunch of times, Clinton would only win about 71.4% of the time. In 28.6% of the “elections” Trump would be elected. A Trump election isn’t surprising.